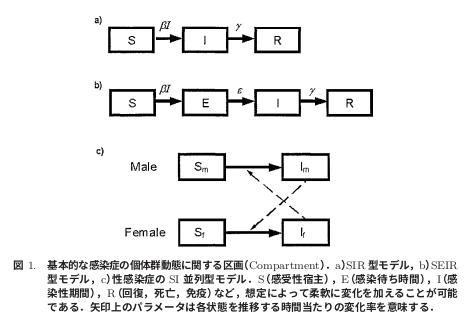
※図1は「感染症流行の予測:感染症数理モデルにおける定量的課題」西浦博、稲葉寿、統計数理(2006)・特集「予測と発見」
から引用させていただきました。
一般的な感染症数理モデルでは、閉鎖集団(Closed population、人の出入りが無く、かつ質が均一な集団、閉鎖人口ともいう)について図1のa)ような区画モデル(compartment model)を想定します。 この区画モデルのことを提唱者の名前からケルマック−マッケンドリック型モデル(Kermack McKendrick model)と呼んだり、各区画の頭文字を取ってSIRモデル(Susceptible-Infectious-Recovered model)と呼んだりします。 (区画モデルについては当館の「統計学入門・第14章第1節 コンパートメントモデル」参照)
ここで、それぞれの区画について次のような仮定をします。
1番目の仮定から、ある時間tにおけるI区画の人数をI(t)と書くと、βI(t)のことを時間tにおける感染力(foece of infection)といいます。 この感染力が大きいほどS区間の多くの人を感染させます。 そしてある時間tにおけるS区画の人数をS(t)と書くと、単位時間あたりの感染者数はβS(t)I(t)になり、この人達がS区画からI区画に移行します。 2番目の仮定から、ある時間tにおける単位時間あたりの隔離+回復+死亡者数はγI(t)になり、この人達がI区画からR区画に移行します。
これらの仮定から、単位時間あたりの各区画の変化人数を各区画の変化速度と考えると、変化速度に関する次のような連立常微分方程式が成り立ちます。
これらの微分方程式を解けば、時間tによる各区画の人数の変化を表す関数S(t)、I(t)、R(t)を決定することができます。 しかしこれらの微分方程式はS(t)、I(t)、R(t)に関して線形ではないので解析的に解くのは困難です。 そこで普通は直接観測することができるI(t)とR(t)の時系列データを用いて、ルンゲ・クッタ(Runge-Kutta)法などの数値計算手法によってパラメータを近似的に求めたり、I(t)を特定の確率分布――例えばポアソン分布や対数正規分布――で近似し、それに基づいてS(t)とR(t)を決定して、最尤法などの確率論的な手法を使って近似的に解いたりします。
そのようにして近似的に解いた結果に基づいて、βとγの値を色々と変えた時のS(t)、I(t)、R(t)の値をプロットすると、色々な場合を想定した時の感染者数の推移をシミュレーションすることができます。 図2はインフルエンザの解析結果を参考にして、S(0)=1、β=0.48、γ=0.29(1/γ=3.5)、R0(基本生産数、第3節参照)=βS(0)/γ=1.7の時の感染者の推移をシミュレーションしたものです。 このグラフを見るとS(t)、I(t)、R(t)の形が何となくわかると思います。 そしてI(t)のグラフは疫学調査で用いられる感染症の流行曲線(Epidemic Curve、エピカーブ)――1日あたりの感染者数を時系列的にプロットしたグラフ――とほぼ同じものになります。
ちなみに上記の連立常微分方程式における比例定数βとγは単位時間あたりの変化率を表し、[1/単位時間]という単位を持ちます。 このような比例定数は感染症モデルだけでなく薬物動態モデルでも、放射性元素の崩壊モデルでも登場し、速度定数(rate constant)とか、崩壊定数(decay constant)とか、時定数(time constant)などと呼ばれています。 (当館の「統計学入門・第14章第1節 コンパートメントモデル」参照)