感染症数理モデル-5

COVID-19の現状分析をした後、まず最初にクルーズ船「ダイヤモンド・プリンセス」のデータに考案した簡易モデルと開発中の統計解析手法を適用してみました。ダイヤモンド・プリンセスは閉鎖集団に近く、しかも流行が始まってから終わるまでのほぼ完全な観測データが得られています。そのため、すでに色々な研究報告が公表されています。そしてそれらの結果と僕の解析結果はよく似ていました。でもその解析結果は某医学研究者が論文に採用する可能性が高いので、残念ながらここでは公表できません。

代わりに1万人あたりの累積感染者数の推移を「DP(人口3777人)」としてグラフ化しておきます。対照集団として中国湖北省の1万人あたりの累積感染者数のグラフを入れておきました。 4章のグラフの縦軸のスケールを50倍にしたので、中国湖北省のグラフはほとんど変化がないように見えてしまいます。日本のインフルエンザについて同じようなグラフを描くと、1年間の累積感染者数が約787人／1万人のところまで上昇します。

ダイヤモンド・プリンセスのデータは感染症数理モデルを当てはめるのに適しているので、少し詳しく説明しましょう。このクルーズ船では2020年2月5日に最初の感染者が発見され、2月15日前後に1日あたりの感染者数がピークになり、2月27日に流行が事実上終息しました。最終的な累積感染者数は696人／3,777人＝約1,876人/1万人で、約19％の人が感染しました。

2章で説明したように、感染の初期段階ではI(t)つまり1日あたりの感染者が指数関数的に増加し、すこし経つと爆発的患者急増(overshoot)段階になります。しかしそれに応じて感染者が増えてS(t)つまり未感染者が減るので、I(t)の増加速度は次第に遅くなり、やがてピークを経てから減少し始め、最終的に流行は自然に終息します。 I(t)がピークになる条件は次の微分方程式から求めることができます。

I区画の変化速度：

I区画の変化速度=0になる時、I(t)がピークになるので

ここで時点tにおける感染者の割合を

とすると

：基本再生産数(1人の感染者が隔離・回復・死亡するまでの間に、何人の人を感染させたかを表す値)

以上から、感染者の割合がp(t)=(1-1/R₀)になった時にI(t)がピークになり、その後は次第に減少することがわかります。この時のp(t)を臨海免疫化割合とか集団免疫閾値(herd immunity threshold)と呼ぶことがあります。例えばR₀=2の時は次のようになり、感染者の割合が50％になった時に1日あたりの感染者数がピークになり、その後は減少します。

一方、流行終息時の感染者の割合を求めてみましょう。 I区画の微分方程式とS区画の微分方程式から、次のような微分方程式が成り立ちます。

　(C：積分定数)
I(0)≒0より

∴

このS(t)とI(t)の関係式を利用すると、両者が時間の経過とともにどのように変化するかを分析することができます。この分析には横軸にS(t)を、縦軸にI(t)を取って、S(t)とI(t)の値をプロットした下の左図「流行の終焉(最終規模方程式)」のようなグラフを用いると便利です。このようなプロットを解曲線または解の軌道(orbit)または解の軌跡(trajectory)といい、これを利用して微分方程式の解の挙動を分析する手法を軌道解析(orbit analysis)または軌跡解析(trajectory analysis)といいます。これは微分方程式の解の挙動を分析する時の常套手段です。

I(∞)≒0より

とすると

∴

→

この式を最終規模方程式(Final size equation)といい、これをグラフ化したものが下の右図「流行強度(最終規模)のR₀応答」です。この方程式から流行終息時の感染者の割合p(∞)はR₀によって決まることがわかります。

※上の2つの図は東京大学大学院・数理科学研究科・稲葉寿教授の「感染症の数理」から引用させていただきました。

上記の最後の2つの式からわかるように、p(∞)からR₀を逆算するのは簡単ですが、最終規模方程式の解を求めること、つまりR₀からp(∞)を求めるのは少々やっかいです。この方程式の解はラグランジュ(Lagrange)の逆公式を用いて、次のような無限級数として解くことができます。ただしこの無限級数を用いた解よりも、ニュートン(Newton)法を用いてR₀から求めた方が実際的です。 (ニュートン法については当館の「統計学入門・付録1　各種の確率分布　(14)各種分布のパーセント点の近似計算」参照)

このようにして求めたp(∞)とS₀から、流行終息時のS(∞)を求めることができます。またS(∞)は上の左図の軌道曲線から推測することも可能です。つまりS(t)とI(t)の軌道曲線は始点が(S(0),I(0)=0)で、終点が(S(∞),I(∞)=0)のため、S(t)とI(t)をプロットすればS(∞)の値を推測することができるわけです。ところがS(t)とI(t)は実際には観測できません。実際に観測できるのはI(t)中の隔離・回復・死亡した人数であるγI(t)つまり単位時間あたりの新規感染者数と、それを累積(積分)したR(t)つまり累積感染者数です。

そこでS(t)とI(t)の代わりにR(t)とγI(t)をプロットした軌道曲線を描いて、軌道解析を行うことが考えられます。 R(t)とγI(t)の軌道曲線は(R(0)=0,γI(0)=0：原点)と(R(∞),γI(∞)=0)の点を通るので、R(∞)つまり流行終息時の累積感染者数を推測することができます。この軌道曲線を用いてCOVID-19の流行の様子を分析している例としては、例えば以下のようなサイトがあります。

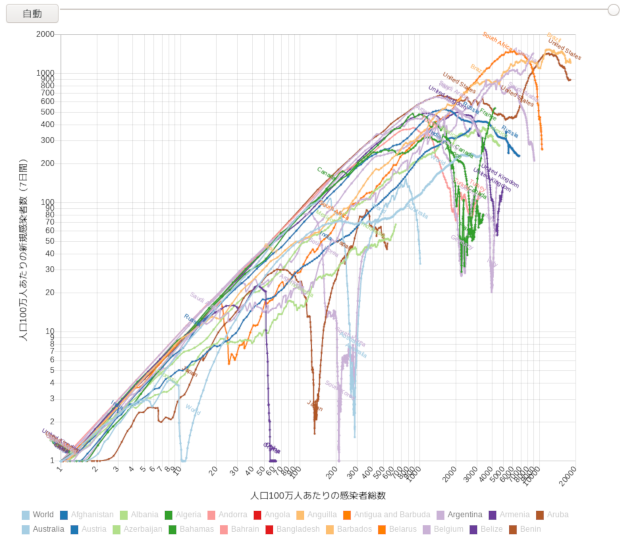
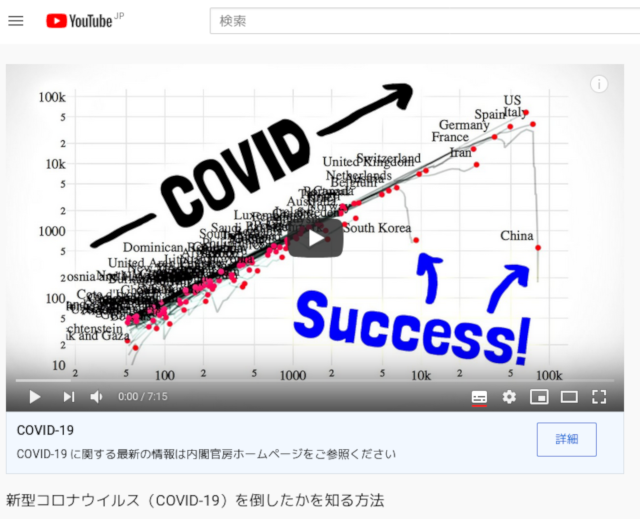
上記の2つのサイトはR(t)とγI(t)を対数変換しています。この理由を、上の動画では「流行初期はR(t)とγI(t)が指数関数的に増加するため」と説明しています。しかし(R(0)=0,γI(0)=0：原点)と(R(∞),γI(∞)=0)の点をグラフ表示するには軌道曲線を実測値で描く必要があります。そのためR(t)とγI(t)を対数変換してはいけません。

また以下のように流行初期はγI(t)≒R(t)になり、軌道曲線は原点を通り、傾きが1の直線状になります。

より

流行初期はγS₀-R(t)≒γS₀だから：

その後はγS₀-R(t)＜γS₀だから：

ここで注意すべきなのは、流行初期におけるR(t)とγI(t)の直線関係は2つの関数の内容とは無関係に成り立つということです。つまり流行初期にR(t)とγI(t)が指数関数的に増加していなくても、その時の軌道曲線は原点を通り、傾きが1の直線状になるわけです。そして流行が進行するとln{(γS₀-R(t))/(γS₀)}項の影響が大きくなり、軌道曲線は傾きが1の直線から離れて低下し、最終的に(R(∞),γI(∞)=0)の点で終わります。

この時、γS₀が小さいとln{(γS₀-R(t))/(γS₀)}項の影響が大きくなるのが早く、軌道曲線は早い時期に傾きが1の直線から離れて低下し、R(∞)の値は小さくなります。その反対にγS₀が大きいとln{(γS₀-R(t))/(γS₀)}項の影響が大きくなるのが遅く、軌道曲線は遅い時期に傾きが1の直線から離れて低下し、R(∞)の値は大きくなります。その様子は、上の「新型コロナウイルス感染者数・死者数のトラジェクトリー解析【国別】」のグラフを見ると何となくわかると思います。

この流行初期に軌道曲線が直線状になる理由と、R(t)とγI(t)を対数変換する点に関して、上の動画の説明は間違っているので注意してください。この動画の製作者は、感染症数理モデルで用いられる軌道解析の内容を知らないのかもしれません。

さて世界各地のデータから、COVID-19のR₀はだいたい2前後と考えられています。そこで上の「流行強度(最終規模)のR₀応答」のグラフでR₀=2の時のpを見ると約0.8です。つまりR₀=2(1人の感染者が2人の人を感染させる)の時、集団の50％の人が感染した時に1日あたりの感染者がピークになり、80％の人が感染すると流行が終息するということになります。

これを日本に当てはめると、累積感染者数が約6,350万人になった時に1日あたりの感染者数がピークになり、1億160万人になった時に流行が終息するという恐ろしいことになります。世界中の感染症専門家がCOVID-19を恐れた理由がわかると思います。

またある集団の中で免疫を獲得した人の割合が集団免疫閾値(臨海免疫化割合)以上になれば、集団に感染者が発生しても流行は起きません。そこで感染症の流行を予防するためにワクチンを接種する場合、R₀に基づいて集団免疫閾値を求め、次のような計算式で予防接種率の達成目標を立てることができます。

ワクチン有効率(vaccine efficacy)：e(0＜e≦1)
ワクチン接種率：p_v(0＜p_v≦1)
基本再生産数：

集団免疫閾値(臨海免疫化割合)：

流行終息条件：

… 予防接種率達成目標
※例えばe=0.8、R₀=2とすると
予防接種率達成目標：

COVID-19について、次のような予想をどこかで聞いたことがあると思います。

「感染予防対策を何もしない時、全人口の60〜80％が感染して免疫を持てば流行が終息する」

この予想を具体的にすると、例えばR₀=2の感染症が流行した時、感染予防対策を何もしないでいると全人口の50％が感染して免疫を持てば流行はピークをすぎ(集団免疫閾値＝臨海免疫化割合)、80％が感染して免疫を持てば流行は自然終息する(最終規模方程式)、ということになります。しかし流行する前にワクチン接種などの方法で人口の50％以上の人が免疫を持てば、感染者が発生しても流行は起きません。

ただしこの場合、感染者が全くいなくなるわけではないことに注意してください。集団免疫を獲得すると、たとえ感染者が出ても、その人が1人以上の人に感染させないので流行が起きないだけであり、感染者が全くいなくなるわけではありません。ワクチン以外の感染予防対策を何もしないでいると、流行はしないものの感染者が出続け、最終規模方程式で求められた割合つまり80％の人が感染すると、ようやく自然終息して感染者が出なくなります。

ダイヤモンド・プリンセスでは流行終息時の感染率は約19％でした。上図のグラフでpが0.19の時のR₀を見ると、だいたい1.1くらいです。そしてR₀=1.1から、I(t)がピークになる時の感染率p_iを求めると次のようになります。

ダイヤモンド・プリンセスで1日あたりの感染者数がピークになったのは、2月15日前後つまり最初の感染者が発見された時から約10日後です。そしてその時の累積感染率は約10％ですから、確かに辻褄が合っています。

ダイヤモンド・プリンセスでは、最初の感染者が発見される前のR_tは10以上あったと推測されています。そして最初の感染者が発見され、検疫・隔離処置がされてから約10日後に1日あたりの感染者数がピークになりました。 COVID-19の潜伏期間と検査が確定するまでの期間を合計すると10日ほどです。そのため検疫・隔離処置によって新たな感染者はいなくなってR_tはほぼ0になり、それから約10日後に感染者が減り始め、流行が終息した時には約19％の人が感染し、流行全体のR_tは1.1程度になったと考えられます。

ダイヤモンド・プリンセスについては、「COVID-19製造機！」とか、「検疫・隔離措置の失敗！」などとマスコミが煽り立てました。しかしデータを詳細に分析すると検疫・隔離措置は見事に成功していて、何もしないでおいたらほぼ全員が感染したところを、検疫・隔離措置によって流行終息時の感染率を約19％に抑えられたということがわかります。

5.最終規模方程式