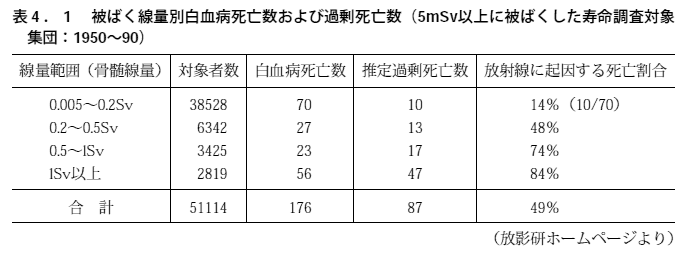

表4.1は被曝量を4段階に分けた時の白血病死亡数と推定過剰死亡数、そして寄与リスク割合を表にし、被曝量とリスクの関係を表したものです。 この表を見ると被曝量が高くなるほど寄与リスク割合の値が大きくなり、被曝量とリスクの間に正比例的な関係があることがわかります。 ただし寄与リスク割合は累積死亡数が少ないほど大きな値になるので、本来なら寄与リスク割合ではなく寄与リスク(絶対リスク)つまり被爆群と非被爆群の累積死亡率の差と被曝量の関係を表にした方が理解しやすいと思います。
表4.1の被曝量を薬剤の用量と考え、死亡数を反応例数とすれば、これは薬剤の用量と反応の関係を表す用量−反応関係になります。 そこで薬剤の用量−反応関係を解析するための手法である用量反応解析をこの表に適用し、被曝量と死亡率の関係を解析してみましょう。 この場合は反応が有無のデータですから、用量反応解析の中のプロビット分析という手法を用います。 (→当館の「統計学入門・第13章 用量反応解析 第4節 プロビット分析」参照)
まず非被爆群の被曝量を0Svとし、その累積死亡率を表4.1の合計欄から計算すると{(176 - 87)/51114}×100=0.174121%になります。 そして4段階に分けた各分類の被曝量を、その線量範囲の真ん中の値にすると、最後の「1Sv以上」以外はそれぞれ(0.005 + 0.2)/2=0.1025Sv、(0.2 + 0.5)/2=0.35Sv、(0.5 + 1)/2=0.75Svとなります。 最後の「1Sv以上」については、資料の「1.1 原爆被爆者調査(82ページ)」の被曝量に関する説明と図4.5から、ここに分類された人の被曝量は1Sv〜4.5Svであり、しかも高線量ほど人数が少なくなると思われます。 そこで、この「1Sv以上」の被曝量を2Svにしてみました。
これらのデータに用量反応解析を適用すると次のような結果になります。 なお以下の表と図は、死亡率(0〜100%)ではなく死亡確率(0〜1)を表しているので注意してください。
| 被曝量(Sv) | 死亡確率(死亡数/対象者数) |
|---|---|
| 0 | 0.00174121(89/51114) |
| 0.1025 | 0.00181686(70/38528) |
| 0.35 | 0.00425733(27/6342) |
| 0.75 | 0.00671533(23/3425) |
| 2 | 0.0198652(56/2819) |
上図の赤色の曲線は、被曝量と死亡確率の関係を累積正規分布という特殊な関数で近似した被曝量−死亡確率曲線です。 それに対して青色の直線は、被曝量と死亡確率の関係を一次関数つまり直線で近似した被曝量−死亡確率直線です。 一見したところ直線の方が近似が良いように見えますが、正確に計算するとどちらもほぼ同程度の近似率です。 座標軸の下部の灰色で表示した領域は、死亡確率に関する医学的な誤差範囲です。 これについては後で詳しく説明します。
このような用量−反応関係を近似する時、見かけ上の近似よりも、近似する関数を理論的に導いた方が合理的です。 そしてそれは次のような考えから導くことができます。
ある人が白血病で死亡する最低の被曝量を、その人の白血病死亡に関する個人的な閾値(いきち)といいます。 例えばある人がお酒を呑んで酔いつぶれる量も、お酒に関する個人的な閾値です。 この閾値は、たった1合で酔いつぶれてしまう”お酒に弱い人”もいれば、1升飲んでも大丈夫という”酒豪”もいるというように、人によって様々です。 それと同様に、白血病死亡に関する個人的な閾値も人によって様々だと思われます。
表4.1の0.005〜0.2Svの欄の死亡した70人の被爆者は、個人的な閾値が浴びた放射線量以下だった人であり、死亡しなかった38458人の被爆者は、個人的な閾値が浴びた放射線量よりも高かった人のはずです。 つまり死亡した70人の閾値は、0〜0.2Svの範囲の色々な値だと思われます(閾値が0Svという人は放射線を浴びなくても死亡する人、つまり放射線以外の要因で白血病死亡する人であり、非被爆群の死亡者は全員がこれに相当します)。
同様に次の0.2〜0.5Svで死亡した27人の閾値は0〜0.5Svの範囲の色々な値であり、0.5〜1Svで死亡した23人の閾値は0〜1Svの範囲の色々な値のはずです。 そうすると、例えば0.5〜1Svの死亡数23というのは、0.5〜1Svの放射線を浴びた被爆者3425人のうち、個人的な閾値が0〜1Svまでの人を合計した数ということになります。 このことから表4.1の4分類の対象者の背景因子がほぼ同じなら、被曝量が高くなるにしたがって死亡率は必ず増加または横ばいになり、減少することはないと考えられます。
そこで被曝量と死亡率の関係ではなく、個人的な閾値と死亡率——実際には対象者の中の同じ閾値の人の割合——の関係を考えることができます。 そしてこの個人的な閾値と死亡率の関係を特定の関数で近似できれば、被曝量と死亡率の関係はその関数を累積したもの、つまりその関数を積分した関数になるはずです。 逆に言えば被曝量と死亡率の関数を微分すると、個人的な閾値と死亡率の関数になるはずです。
その考えからすれば、被曝量と死亡率の関係を直線で近似した時は、個人的な閾値と死亡率の関係は定数になる、つまり個人的な閾値は被曝量とは無関係に常に一定の割合であり、それを累積するから被曝量と死亡率の関係が直線になる、ということになります。 これは、例えば上図のように個人的な閾値が0Svの人の割合は別にして、1Svの人の割合も、2Svの人の割合も、5Svの人の割合も全て同じということであり、常識的にはあまり考えられません。
例えばお酒に関する個人的な閾値は人によって様々でしょうが、たった1合でつぶれてしまう”お酒に弱い人”の割合や、1升飲んでも大丈夫という”酒豪”の割合は比較的少なく、平均的な閾値付近の人の割合が最も多いでしょう。 それと同様に白血病死亡に関する閾値も、例えば上図のように、個人的な閾値が0Svの人の割合は別にして、平均的な閾値付近の人の割合が最も多く、それよりも小さい閾値の人の割合も、それよりも大きい閾値の人の割合も徐々に少なくなっていくと考えられます。
その様子を理論的な関数で表したものが正規分布と呼ばれるベル型の曲線です。 そしてその正規分布を積分した関数が累積正規分布であり、S字状の曲線(シグモイドカーブ)になります。 図10.2.1の赤色の曲線が累積正規分布であり、図10.2.2の赤色の曲線が正規分布です。 (→当館の「統計学入門・第10章 ロジスティック回帰分析 第2節 各種のシグモイド曲線 図10.2.1と図10.2.2」参照)
累積正規分布曲線は、死亡率(図10.2.1では出現率)が非常に小さい部分は傾きが小さい直線で近似でき、死亡率が急に上昇する部分は二次曲線(放物線)で近似でき、死亡率がだいたい0.2(20%)〜0.8(80%)の部分は傾きが急な直線で近似でき、全体として0.5を中心にして点対称(0.5を中心にして回転すると同じ形になる)になっています。 用量−反応関係をこの累積正規分布曲線で近似するモデルをプロビットモデルといい、プロビットモデルを利用して用量−反応関係を解析する手法をプロビット分析といいます。
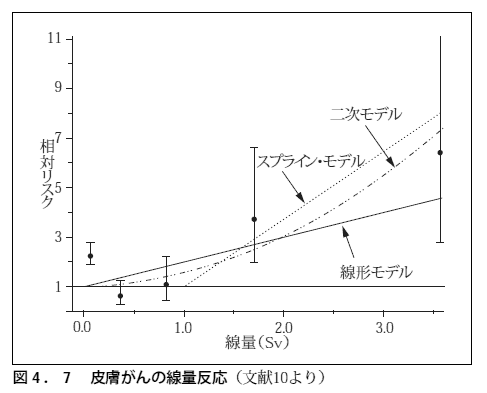
資料の図4.7で、皮膚がんの線量反応関係を3種類のモデル(関数)で近似しています。 この中の線形モデルはプロビットモデルの死亡率が非常に小さい部分を直線で近似したものに相当し、二次モデルはプロビットモデルの死亡率が急上昇する部分を放物線で近似したものに相当し、スプラインモデルはプロビットモデルの死亡率が非常に小さい部分と、死亡率が直線的に増加していく部分を2種類の直線で近似したものに相当します。
この寿命調査ではポアソン回帰分析を利用して死亡率を解析しています。 死亡率が低い時、死亡率は指数関数的に変化することが多いため、ポアソン回帰分析は死亡率の変化を指数関数で近似します。 つまり寿命調査の解析では、実は指数関数モデルを採用しているわけです。 しかし図4.7には指数関数モデルはプロットされていないため、この図は用いた統計手法と少々矛盾しています。 指数関数モデルはプロビットモデルの死亡率が非常に小さい部分と、死亡率が急上昇する部分を近似したものに相当します。 (→当館の「統計学入門・第15章 ポアソン回帰分析」参照)
資料ではプロットとモデルの見かけ上の近似性だけを検討していて、個人的な閾値のことは検討していません。 個人的な閾値のことを考えると、線形モデルも二次モデルもスプラインモデルも指数関数モデルも、個人的な閾値の理論的関数である正規分布のある部分だけを近似したモデルになり、どのモデルも部分的に近似するだけで全体的に近似するわけではないことがわかります。 つまり個人的な閾値の関数から被曝量と死亡率の関数を理論的に導くと累積正規分布になり、4種類のモデルは全てプロビットモデルの部分的な近似モデルであることがわかると思います。
そして線形モデルは線量が少ない時は実際の線量反応関係とある程度近似しますが、図4.7からわかるように線量が多くなるとズレが大きくなり、リスクを過小評価してしまう危険性があることに注意する必要があります。 国際放射線防護委員会は放射線防御という観点から、安全性を重視して「被曝量とガン死亡率の関係は直線であり、集団の閾値はない」というLNT仮説(Linear Non-Threshold hypothesis)を採用したと言われています。 しかしこの仮説に基づいた線形モデルは線量が高くなるとリスクを過小評価してしまう危険性があり、決して安全ではありません。 どの線量領域でも実際の線量反応関係と近似の良いプロビットモデルの方が、実は安全なのです。
またこの図4.7は被曝量と相対リスクの関係をプロットしていますが、相対リスクは死亡率が直線的に変化すると双曲線的に変化するので、被曝量−反応関係を解析するには適していません。 やはり被曝量と死亡率そのものをプロットした方が合理的です。
放射線の健康被害について、白血球や赤血球の減少といった急性影響については確定的影響として閾値があると考え、発ガン性のような晩発影響については確率的影響として閾値がないと考えるのが、放射線防御の観点での主流の考え方です。
ここでいう「閾値」は、個人的な閾値ではなく集団の閾値のことです。 集団の閾値とは、ある集団の中の1人以上が急性影響または晩発影響を受ける最低の被曝量のことであり、それは集団に属す人の個人的な閾値の最低値になります。 そして「閾値がない」とは「集団の閾値がない」ということであり、ほんのわずかでも放射線を浴びれば影響を受ける人が必ず存在する、つまり個人的な閾値の最低値は無限小であるということです。
統計学的な観点からは、急性影響は放射線を浴びない時の発生率が事実上0%のため集団の閾値が判別しやすいのに対して、晩発影響は放射線を浴びない時の発生率が0%ではないため集団の閾値が判別しにくいという違いがあるだけで、どちらも個人的な閾値に基づいた被曝量−反応関係という点では同じです。 そしてたった1滴のお酒で酔いつぶれてしまう人がいないのと同様に、個人的な閾値の最低値が無限小ということは現実にはほとんど有り得ません。
ただし、ある人が発ガンする最低の被曝量が存在せず、被曝量とは無関係にランダムに発ガンすると仮定すると、個人的な閾値というものは存在しなくなります。 そして個人的な閾値が存在しなければ、当然、集団としての閾値も存在しません。
しかし個人が被曝量とは無関係にランダムに発ガンすると、集団の発ガン率は被曝量とは無関係に一定になり、被曝量が多いほど発ガン率が高くなるという関係は生じないはずです。 このことから放射線の晩発影響についてもやはり個人的な閾値が存在し、それによって被曝量が多いほど発ガン率が高くなるという被曝量−反応関係が導かれると考えた方が妥当でしょう。
用量反応解析で求めたプロビット曲線を利用すると、低放射線量被曝の死亡率を推測することができると同時に、集団の閾値を推測することができます。 ただしプロビット曲線の元となる閾値の正規分布は、個人の閾値が0Svから無限大まで存在するという仮定基づいた分布です。 そのためプロビット曲線は被曝量が0Svの非被爆者集団の死亡率を起点として、被曝量が増加するにしたがって死亡率が必ず増加するため、集団の閾値は理論的に0Svになります。 つまりプロビットモデルは、LNT仮説と同様に「集団の閾値はない」という仮定に基づいたモデルなのです。
そこで相対リスクの値から放射線の影響を判断した時のように、この場合も死亡率の数学的な誤差範囲である信頼区間と、医学的な誤差範囲の両方に基づいて集団の見かけの閾値——この値未満では放射線の影響を事実上判断できない被曝量——を求める方が実際的です。
非被爆群の死亡率は0.174121%ですが、この90%信頼区間を計算すると0.143〜0.205%になります。 プロビット布曲線を利用して、死亡確率がこの信頼区間の上限値である0.205%つまり0.00205になる時の被曝量を逆算すると0.0959Sv(95.9mSv)になります。 このことから0.0959Sv(95.9mSv)未満の被曝量については、その影響を統計学的に判断できないことになります。
一方、医学的な誤差範囲は、例えば次のようにして推測します。 0.174121%という死亡率は、41年間で1万人あたり17人の死亡があったという意味です。 すると、1年間では平均して10万人あたり4人の死亡があったことになります。 このことから、仮に1年間で10万人あたり±1人の死亡数の変動は医学的な誤差範囲である、つまり診断誤差や死因の特定誤差を考慮すると、この程度の増減は医学的には誤差範囲であり、死亡率の増減を判断できないとします。 すると41年間では10万人あたり±41人の死亡、つまり±0.041%の変動は誤差範囲ということになります。
この医学的な誤差範囲を非被爆群の死亡率に適用すると、0.174121±0.041%つまり0.133121〜0.215121%の範囲内の変動は実質的に死亡率の増減を判断できないことになります。 プロビット曲線を利用して、死亡確率がこの誤差範囲の上限値である0.215121%つまり0.00215121になる時の被曝量を逆算すると、0.130418Sv(130.418mSv)になります。
この閾値と信頼区間から求めた閾値を比べると、この閾値の方が被曝量が多くなっています。 このことから集団の見かけの閾値は約0.13Sv(130mSv)であり、これより低い被曝量の時は白血病の死亡率の増減を事実上判断できないということになります。 一番上の被曝量と白血病のグラフで、座標軸の下部に灰色で表示した範囲が死亡確率に関する医学的な誤差範囲であり、赤色のプロビット曲線がこの範囲に入る時の被曝量が事実上の閾値になり、この灰色の範囲内では死亡率の増減を明確には判断できないわけです。
また死亡率の増加が実質的に特に問題となる被曝量は、プロビット曲線が急上昇する被曝量以上の時です。 上図のグラフから、プロビット曲線が急上昇するのは1Sv付近であり、これ以上の被曝量の時は特に注意を要することがわかります。
ただし1Svの被曝量の時のガン死亡率の増加は、喫煙によるガン死亡率の増加の半分程度です。 喫煙者の周囲にいる人間が、喫煙者の吐き出すタバコの煙を吸ってしまうことを受動喫煙といいます。 受動喫煙によるガン死亡のリスクは喫煙のリスクのだいたい10分の1から2分の1程度と言われているので、200mSv〜1Svの放射線被曝のリスクに相当します。
そのため50mSv程度の放射線被曝をする危険性がある禁煙場所から、放射線被曝の危険性はないものの、喫煙者がいる避難場所に避難するとかえってガン死亡のリスクを上げてしまうことになります。
また野菜不足によるガン死亡のリスクは喫煙によるガン死亡リスクの20分の1程度であり、計算上は100mSvの被曝量の時のガン死亡のリスクと同程度です。 したがって1mSv程度の内部被曝をする危険性を恐れて野菜を食べないでいると、かえってガン死亡のリスクを上げてしまうことになります。(→国立がん研究センター「わかりやすい放射線とがんのリスク」)
現在は、ある場所に1年間いた時に、50mSv以上の被曝の可能性がある場合は避難指示が出されます。 また食品については、ある食品を一定の量だけ1年間食べ続けた時に、1mSv以上の内部被曝の可能性がある場合は出荷制限されます。
これは発ガン性のような晩発影響については集団としての閾値がない、つまりたとえ1mSvの被曝量でもガン死亡のリスクが上昇するという放射線防御の観点での考え方と、100mSv以下の被曝量ではガンの明確なリスク上昇は医学的に判断できないというこの原資料の結果と、さらに自然放射線による日本人の平均的な被曝量は1年間で1mSv程度であるという事実を総合的に考慮して決められたものです。
しかしこの原資料の結果から、これらの基準は非常に安全側に立った基準であることがわかると思います。 放射線被曝を避けるための行動は、こういったことを総合的かつ冷静に判断して行う必要があります。 甲状腺被曝を恐れて毒性の強いヨードチンキを飲んだり、飲料水を飲まずに脱水症状になったり、野菜を食べずに野菜不足になったりと、マスコミ報道に煽られて闇雲に行動するとかえってリスクを上げてしまう結果になりかねません。