ワクチンの有効性と安全性-4

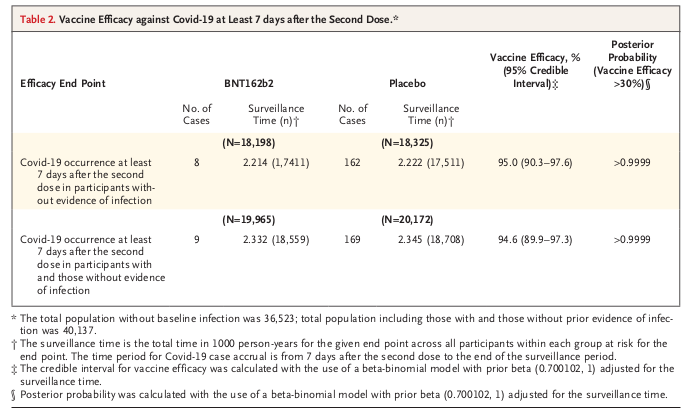
Table2のワクチン有効率(Vaccine Efficacy)については、前章までの説明である程度は理解できたと思います。でもその後ろに記載されている95％ベイズ信用区間(95％ Credible Interval)と、ワクチン有効率が30％より大きい事後確率(Posterior Porbability)は理解するのがかなり難しいと思います。

・BNT162b2接種群：例数=18,198　感染例数=8　観測期間(Surveillance Time)=2.214(追跡例数=17,411)
・プラセボ接種群：例数=18,325　感染例数=162　観測期間=2.222(追跡例数=17,511)
　ワクチン有効率=95.0％　95％ベイズ信用区間(Credible Interval)=90.3-97.6％
　ワクチン有効率が30％より大きい事後確率(Posterior Porbability)＞0.9999

95％ベイズ信用区間は一般的な95％信頼区間にほぼ相当します。つまりワクチン有効率には誤差があり、本当のワクチン有効率は最低90.3％から最高97.6％の間である確率が高い(95％程度)という意味です。

そして「事後確率＞0.9999」は一般的な「有意確率 p＜0.0001」にほぼ相当します。つまり「ワクチン有効率は30％よりも大きい」ということが有意水準0.0001以下で有意である、すなわちワクチン有効率が30％以下である確率は0.0001(0.01％)よりも小さく、「ワクチン有効率は30％よりも大きい」ということが0.9999(99.99％)以上の確率で言えるという意味です。これらはベイズ統計学(Bayesian Statistics)で用いられる手法です。 (ベイズ統計学については当館の「統計学入門・第11章第6節　付録6　ベイズ統計学」参照)

ベイズ統計学はベイズの定理に基づいた統計学であり、一般的な信頼区間CI(Confidence Interval)の代わりにベイズ信用区間CI(Credible Interval)またはベイズ確信区間を求め、有意確率p値を利用した一般的な統計的仮説検定の代わりにベイズ因子(Bayes factor)または事後確率(Posterior Porbability)を利用したベイズ流検定を行います。

近頃、製薬企業が実施する臨床試験でベイズ統計学を用いるのが流行しています。その理由は、ベイズ統計学は結果をある程度恣意的に変えられるからです。

例えばTable3の一番上の「Over all(全体)」の行はTable2の上段の結果と同じものです。しかしTable3のワクチン有効率の95％信頼区間(95％ CI)は90.0-97.9％になっていて、Table2の95％ベイズ信用区間90.3-97.6％よりもわずかに広くなっています。この理由は、Table3は一般的な95％信頼区間を求めているからです。 Table2のベイズ信用区間は事前情報を用いることによって信用区間の幅を少し狭くし、誤差が少なくて信頼性が高いような印象を与えているのです。

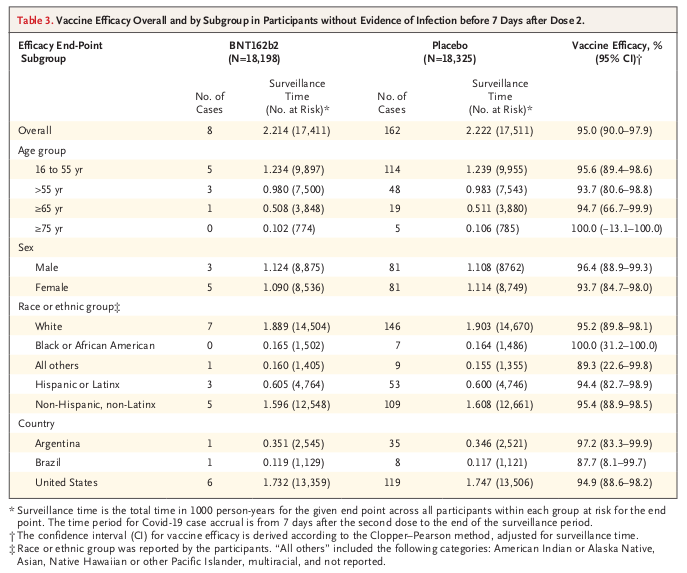
この臨床試験ではワクチン有効率そのものが高いので、一般的な信頼区間とベイズ信用区間の違いはわずかです。でもワクチン有効率が低い時は一般的な信頼区間とベイズ信用区間の違いがもっと大きくなり、ベイズ信用区間を用いることによって結果の信頼性が高いような印象を与えることができます。そしてベイズ統計学について正確に理解している医学研究者は少ないので、製薬企業が実施する臨床試験でベイズ統計学が流行しているわけです。

なおTable2でベイズ信用区間を用いたのなら、Table3も同じ手法を用いなければ整合性が取れません。しかしTable3は層別解析(サブグループ解析)――被験者を年齢や性別で複数のグループに分けて解析する方法――なので、信用区間を求める項目が沢山あります。そしてベイズ信用区間は計算がやたらと面倒な割に、一般的な信頼区間との違いに気づく医学研究者は少ないと考えられます。そのためファイザーの解析担当者は、Table3については手抜きをして一般的な信頼区間を求めたのではないかと思います。

事実、これまでに僕が読ませていただいた、医学研究者の方が書かれたこの論文の解説で、Table2のベイズ信用区間を正確に説明したものはなく、Table2のベイズ信用区間とTable3の信頼区間がわずかに異なっていることを指摘し、その理由を説明したものも残念ながらありませんでした。

一般的な統計学つまりネイマン・ピアソン統計学とベイズ統計学の違いは、大雑把に言えば先行研究から得られた事前情報の扱い方の違いです。 ネイマン・ピアソン統計学では事前情報をそのまま信用せず、それに基づいて仮説を組み立て、客観的なデータによってその仮説の真偽を検証します。これは自然科学で用いられる仮説演繹法の手順に従ったものであり、近代科学の基本的な思考法である批判的思考法(critical thinking)に基づいています。

それに対してベイズ統計学では事前情報を信用し、それに客観的なデータを組み合わせることによって事前情報をより確実性の高いものに更新していきます。これは我々が日常的に行っている経験的思考法に基づいたものであり、普通の人にはネイマン・ピアソン統計学よりもむしろ馴染みやすいと思います。しかし事前情報を恣意的に決めることができるので、どうしても主観的になりがちです。

自然科学分野では、画期的な観測方法が発明されて新しい観測データが得られると、それまでの自然観が覆されて全く新しい自然観が誕生するパラダイムシフトが起きることがたまにあります。

例えば天動説から地動説へのパラダイムシフトがその代表例です。このパラダイムシフトは経験的思考法ではなかなか起こりません。つまり素朴な観測結果に基づいた天動説という事前情報を正しいと考えると、望遠鏡の発明によって新しい観測データが得られても、プトレマイオスの周転円を用いた精緻な天動説モデルは導けますが、天動説という事前情報を真っ向から否定する地動説は導けないのです。

地動説を導くためには天動説という事前情報をそのまま信用せず、それを単なる仮説と考え、新しい観測データに基づいて批判的に検討する必要があります。そこで近代科学は経験的思考法の代わりに批判的思考法を重視し、仮説演繹法という厳密な手順を確立しました。 (仮説演繹法については当館の「統計学入門・第1章第8節　1.8 科学的研究の種類　(1)仮説演繹法」参照)

ところが客観的な情報が少なく、個人の経験やカンに基づいた情報に頼りがちな分野――例えば社会学分野等――では、批判的思考法よりも経験的思考法の方が馴染みやすいところがあります。そのため経験的思考法に基づいたベイズ統計学が向いています。

ベイズ統計学は事前情報を恣意的に設定することによって、結果を恣意的に変えることが可能です。そのため臨床試験の結果を恣意的に変えたい製薬企業にとっては実に有り難い手法であり、近頃、とみに流行しています。そして製薬企業で流行しているということは、とりもなおさず消費者にとってあまり好ましくない手法なのです。

4.ベイズ統計学